Milestones:Invention of Temparature- Insensitive Quartz Oscillation Plate Enabling HIghly Stable Communications and Clocks, 1933

Title

Invention of a Temperature-Insensitive Quartz Oscillation Plate, 1933

Citation

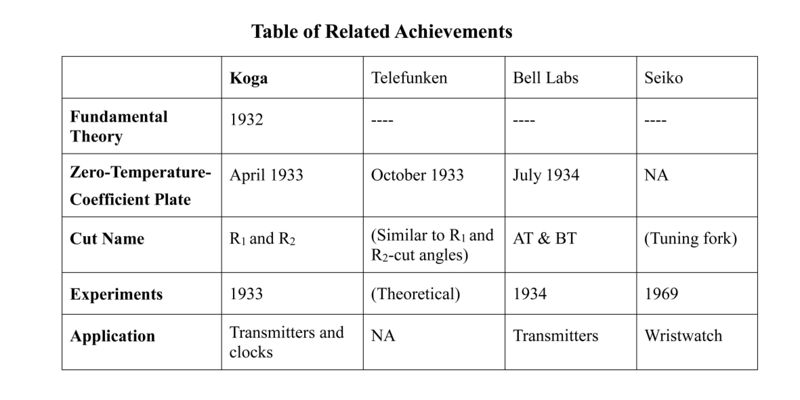
In April 1933, Issac Koga of the Tokyo Institute of Technology reported cutting angles that produced quartz crystal plates having a zero temperature coefficient of frequency. These angles, 54⁰ 45’ and 137⁰ 59’, he named the R₁ and R₂ cuts. Temperature-insensitive quartz crystal was used at first for radio transmitters and later for clocks, and has proven indispensable to all radio communication systems and much of information electronics.

Street address(es) and GPS coordinates of the Milestone Plaque Sites

35.606876, 139.684802,

Tokyo Institute of Technology Museum

2–12–1, O-okayama, Meguro-ku, Tokyo, 152-8550 Japan

GPS: 35.606876, 139.684802

Details of the physical location of the plaque

In a special showcase at the Exhibition Room of the Institute Museum

How the intended plaque site is protected/secured

The Museum is open to the public on weekdays from 10:30 to 16:30. (Closed nights and holidays.)

Historical significance of the work

Its technological, scientific, and social importance may be described as follows:

(1) Pioneering theoretical analysis of the thickness vibrations of quartz oscillation plates

Quartz oscillation plates being used in the early 1930s were almost entirely limited to X-cut and Y-cut plates (X and Y axes are perpendicular to the Z-axis). The characteristics of these plates were only known after sectioned measurement. Meanwhile, the resonant frequency of vibration of any isotropic plate is well known and is expressed by:

where "f" is resonant frequency, "a" is plate thickness, "ρ" is density, "c" is the adiabatic elastic constant of the medium, and "q" is any integer.

At that time there was no apparent vibrational expression for anisotropic media. In order to overcome this situation, Issac Koga attended to a theoretical analysis of the vibration of quartz crystal plates [1].

In 1932, based on equations for thickness vibration that he derived using the general equation for motion in any anisotropic crystalline medium, Koga showed that there could exist three normal modes of thickness vibration.

In August of that year, he derived a significant formula for elastic constant "c" in Eq. (1) corresponding to the thickness vibration in the case of a quartz crystal plate cut parallel to the X-axis and having its rotating angle θ about the X-axis. The requisite coefficient c^eq is given by the following equation:

where c_ij are adiabatic constants of crystal depending on plate orientation with respect to the crystallographic axes of the medium [2, 3].

Thus by employing "c^eq" in place of "c" in Eq. (1) Koga expressed the vibrational characteristics of crystalline media as follows:

This formula being simple, but containing sufficient information, was published in 1932 for the first time in history. It has been widely referred to by numerous researchers both inside and outside Japan as described below and has become the basis for subsequent development of quartz plates, achieving desired frequencies as well as lower temperature coefficients.

(2) Invention of quartz crystal plates with zero temperature-coefficient

"In the early 1930s most oscillators in transmitters used in short-wave radio telecommunications employed the X- or Y-cut plates that were relatively sensitive to temperature variation. Therefore temperature-regulating equipment was indispensable. The use of thermostats for this purpose included such problems as long start-up time and frequent maintenance. Accordingly, demand for quartz crystal plates with a smaller temperature coefficient was increasing.

Several ideas (for example, ring shaped plates) were tried in order to achieve zero temperature-coefficients, but no practical solution for transmitter use was found.

Around 1930, Issac Koga noticed that the crystallographic face r of positive rhombohedrons displayed various unique characteristics [4]. He believed that plates cut out in parallel to the face r might possess special properties for oscillators, namely R-cut plates (cf. Fig. 1 Media:Fig_1.pdf). Similarly, those plates cut out in parallel to the r' face (reverse side of r face) were thus termed R'-cut. He found several advantages in these R- and R'-cut plates, such as easier excitation, strong oscillatory power, and a smaller temperature-coefficient than for conventional X- and Y-cut plates. He obtained a Japan Patent for this R-cut in April 1932 [5].

After the discovery of R-cut and R'-cut, Koga noticed the fact that R'-cut plates have a negative temperature coefficient while the Y-cut yields a positive one. Therefore, he hypothesized the existence of a zero-temperature-coefficient plate between them. He tested plates by rotating the cutting angles around the X-axis from R'-cut (cf. Fig 1, θ = 51°) to Y-cut (θ = 90°). Koga and his colleague Ichinose clarified the existence of a zero-temperature-coefficient plate (at around θ = 55°) in their report published in April 1933 for the first time [6] (cf. Fig. 2 Media:Fig_2.pdf ).

Through continued precise theoretical investigation and experiments, Koga discovered the existence of two cutting angles arriving at a zero temperature-coefficient. Pursing closer studies in the region of θ = 55°, a precise angle of 54° 45′ was determined. These results were reported on October 10, 1933 [7].

In parallel with his theoretical work, Koga proceeded to produce a practical plate with a zero-coefficient. Finally, for the first time anywhere in the world, he realized a very low temperature-coefficient plate on the order of 10^-7, while conventional ones (X- and Y-cut, among others) were on the order of 10^-5. This result was also included in the above-mentioned report of October 10, 1933 [7]. Slightly different examples of quartz plate holders used in Koga's research are shown in Fig. 3 Media:Fig_3.pdf and Fig. 4 Media:Fig_4.pdf.

Some ten days after Koga's announcement, a similar theoretical prediction (the existence of two types of zero-temperature-coefficient plates) was reported on October 20, 1933 by a German researcher, R. Bechmann of Telefunken Co. In this report, Koga's earlier paper written in 1932 [3] was cited as a reference, an event detailed below in the present document.

Koga discovered another possible zero-temperature-coefficient angle: 137°59′. That work was published in December 1933 [8]. It was these cuts that were later called R₁- and R₂-cut, respectively.

In July 1934, a similar result for zero-temperature-coefficient plates was reported in the Bell System Technical Journal under the names of AT- and BT-cut. This nomenclature remains in use today, but is substantially the same as Koga's R₁- and R₂-cuts -common enough occurrence in scientific and engineering fields.

(3) Development and practical design of crystal clocks in Japan using stable quartz oscillators

Koga believed from the earliest stage of his research on quartz oscillation that one important application areas would be crystal clocks, able to provide dependable time and frequency standards.

He proposed and developed various types of crystal clocks using his stable oscillation plates. The first model (KQ-1) was designed in 1936 and first demonstrated at the 1937 Paris International Exposition (Fig. 5 Media:Fig_5.pdf). He continued the improvement of quartz clocks (models KQ-2 to KQ-5) until the 1950s in cooperation with Tokyo Astronomical Observatory (Fig. 6 Media:Fig_6.pdf). The final model (KQ-6) was designed in 1955 for professional uses. It was installed in Kokusai Denshin Denwa Co., Ltd. (KDD), where it operated satisfactorily for more than ten years as a time-and-frequency standard (note Fig. 7 Media:Fig_7.pdf and Fig. 8 Media:Fig_8.pdf).

(4) Social importance of the invention of temperature-insensitive quartz crystal oscillation plates

Utilization of quartz oscillation plates having zero temperature-coefficient of frequency has made possible the elimination of inconvenient temperature regulators (thermostats) in telecommunication stations. This is especially important for mobile and portable radio communication systems.

At the present time, the generation of stable frequency signals by quartz crystal is indispensable in such applications as smartphone, Internet, and PC. It is not too much to say that our current daily lifestyle would be unimaginable without temperature-insensitive quartz technology applications.

Several examples of oscillation plates (from past to present-day) are shown in Fig. 9 Media:Fig_9.pdf. The current worldwide distribution of quartz-based industries is displayed in Fig. 10 Media:Fig_10.pdf.

All Figures of Fig. 1 to Fig. 10 refered in the above paragraphs are shown with the following linking .

Media:Fig.1_to_Fig.10.pdf

Features that set this work apart from similar achievements

(1) Koga's achievement

Issac Koga started his study of quartz crystal oscillators following Cady's initial discovery (1922) of quartz plate oscillation. At that time, investigations of quartz oscillation were mostly undertaken experimentally by making actual oscillation plates without any back-up design principle. In order to overcome the inherent complexities, Koga strove successfully to establish a precise theory for the vibration analysis of quartz plates.

Koga's work may be summarized as follows:

*Theory of crystal vibration

In 1932, when Koga established his precise theoretical analysis of thickness vibration of anisotropic quartz crystal, no similar theory existed. Therefore, Koga's theory [2 and 3] was readily adopted in the field together with the practice of rotating the cutting angle around the crystallographic axis. This contributed worldwide to the application of zero-temperature-coefficient quartz plates.</dev>,br />

*Zero-temperature-coefficient plates

In late 1929 and early 1930, several proposals appeared for realization of zero-temperature-coefficient plates. Among them, a ring-type plate was considered promising, however it was unusable in actual transmitters owing to delicate design constraints.

As explained, Koga concentrated on producing a zero-temperature-coefficient plate by rotating the cutting angle along the X-axis and realized an actual plate having a zero-coefficient in 1933 [7]. Similar work was being done in Europe and US, and this may be summarized as follows:

(2) Early work in Germany

After Koga's realization of zero-temperature-coefficient (in fact, “near-zero”) plates on October 10, 1933, Bechmann of Telefunken Co., independently reported theoretical prediction of the existence of two types of zero-temperature-coefficient plates. In this report, Koga's 1932 paper [3] was offered as a starting point. (cf. Naturwissenschaften, Vol. 21, No. 42, p. 752, October 20, 1933)

(3) Successive work at Bell Labs (US)

In July 1934, Lack, Willard, and Fair of Bell Laboratories in the US reported zero-temperature-coefficient plates by rotating the cutting angle about X axis starting from Y-cut crystals. The two types of plates were named AT- and BT-cut. Presently the terms AT and BT are still widely used, however they are substantially the same as Koga's earlier respective R₁- and R₂-cut (cf. Bell System Technical Journal, p. 453, July 1934).

(4) Seiko's IEEE Milestone: Quartz Wristwatch

The wristwatch achieved by the firm of Suwa Seikosha in 1969 has already been filed as an IEEE Milestone (2004). In this case, quartz oscillators use a different type of vibration mode, namely a tuning-fork. This is because frequency must be lower (some 32 kHz) than that used for communication purposes in order be accommodated within a very compact space.
Although Koga proposed tuning-fork vibration components in his studies before hitting upon a strict zero-temperature-coefficient vibrator R₁-cut, the significance of the present Milestone Proposal differs greatly from that awarded Seiko. Therefore, the wristwatch Milestone in no way detracts from the originality of the present Issac Koga proposal.

Koga's pioneering studies in the theory and technologies of quartz oscillation continued unabated, in collaboration with his group (cf. Fig. 11 Media:Fig_11.pdf) after World War II (including [11] and [12] Media:Fig_12.pdf). These works have further contributed to the establishment of present-day quartz technologies.

Significant references

(Note)
In the references listed below, Koga's affiliated university name “Tokyo University of Engineering” refers to the older English appellation of the present-day “Tokyo Institute of Technology”.

(Theory of Vibration Analysis)

[1] I. Koga, "Longitudinal Vibration of Short Circular Cylinders" (in Japanese), Journal of the Institute of Electrical Engineers of Japan, Vol. 50, No. 508, pp. 1209-1224, November 1930.

[2] I. Koga, "Thickness Vibration of Piezoelectric Oscillating Crystal", Physics, Vol. 3, No. 2, pp. 70-80, August 1932.

[3] I. Koga, (the same item as Ref. [2], in English), Report of Radio Researches and Works in Japan, Vol. II, No. 2, pp. 157-173, September 1932.

(Zero-Temperature-Coefficient Oscillation Plates)

[4] I. Koga, "R-cut Quartz Oscillating Plates and Harmonic Oscillation (in Japanese)", Proc. of 2nd Conference on Engineering, Electrical Engineering Section, No. 102, p. 170, April 1932.

[5] Japan Patent No. 95637, "Piezoelectric Vibration Plates", Koga (inventor), Takeuchi (patentee), April 30, 1932 (granted).

[6] I. Koga and K. Ichinose, "Quartz Oscillating Plates with Small Temperature Coefficients for Short-Wave" (in Japanese), Proc. of 8th Joint Conference on Electrical Engineering, No. 135, pp. 205-206, April 2, 1933.

[7] I. Koga and N. Takagi, "Piezoelectric Oscillating Quartz Plates with Temperature Coefficients less than 10^-7/°C" (in Japanese), Journal of the Institute of Electrical Engineers of Japan, Vol. 53, No. 543, p. 940, October 10, 1933.

[8] I. Koga and N. Takagi, "Temperature Coefficients of Elastic Constants of Quartz" (in Japanese), Journal of the Institute of Electrical Engineers of Japan, Vol. 53, No. 545, p. 1141, December 1933.

[9] I. Koga, "Thermal Characteristics of Piezoelectric Oscillation of Quartz Plates", Report of Radio Researches and Works in Japan, Vol. 4, No. 2, pp. 61-76, February 1934.

(Quartz Clock)

[10] I. Koga, "Quartz Electric Clock" (in Japanese), OHM, Vol. 25, No. 5, pp. 425-426, May 1938.

(Subsequent Studies on Quartz Crystal)

[11] I. Koga and H. Fukuyo, "Vibration of Thin Piezoelectric Quartz Plates (Especially on R₁ -Cut Rectangular Plates" (in Japanese), Journal of the Institute of Electrical Communication Engineers of Japan, Vol. 36, No. 2, pp. 59-67, February 1953.

[12] I. Koga, M. Aruga and Y. Yoshinaka, "Theory of Plane Elastic Waves in a Piezoelectric Crystalline Medium and Determination of Elastic and Piezoelectric Constants of Quartz", Physical Review, Vol. 109, No. 5, pp. 1467-1473, March 1958.

Supporting materials