Milestones:Shannon
This is a temporary page. The final version of this page can be found on the Engineering and Technology History Wiki
Title
Development of Information Theory, 1939-1967
Citation
The mathematical principles of Information Theory, laid down by Claude Elwood Shannon over the period 1939-1967, set in motion a revolution in communication system engineering. They quantified the concept of information, established fundamental limits in the representation and reliable transmission of information, and revealed the architecture of systems for approaching them. Today, Information Theory continues to provide the foundation for advances in information collection, storage, distribution, and processing.
Street address(es) and GPS coordinates of the Milestone Plaque Sites
42.360397, -71.094217, Research Laboratory of Electronics Massachusetts Institute of Technology 50 Vassar Street, Cambridge, MA, 02139 Lattitude, Longitude: 42.360397, -71.094217 N42° 21.6238', W71° 5.653'
Details of the physical location of the plaque
The plaque is to be displayed on the wall along an interior corridor of the Laboratory, on the floor and in close proximity to where Claude Shannon's office was located while he was at MIT.
How the intended plaque site is protected/secured
The corridor is well-trafficked and accessible to general public at all times without the need for appointments or other special arrangements. The campus buildings are all monitored by campus police.
Historical significance of the work
Before the development of information theory, communication system engineering was a largely heuristic engineering discipline, with little scientific theory to back it up or guide the architecture of such systems.
By 1940, a large number of communication systems existed, major ones including Telegraph, Telephone, AM Radio, Television, etc. These systems are very diverse and separate fields emerged to deal with each of them, using their own set of tools and methodologies. For example, it would have been inconceivable that one would be able to send video over a phone line, as is commonplace today with the advent of the modem. Engineers at that time treated video transmission and telephone technology as separate entities and did not see the connection as simply the transmission of `information’—a concept that in time would cross the boundaries of these disparate fields and bind them together.
In his development of information theory, Shannon was the first person to quantify the notion of information and provided a general theory that reveals the fundamental limits in representation and transmission of information. Information theory as proposed by Shannon, in the broadest sense, can be divided into two parts: 1) that of conceptualization of information and the modelling of information sources and 2) that of reliable transmission of information through noisy channels as next described.
1) Shannon echoed the viewpoint established by Hartley that the information content of a message has nothing to do with its inherent meaning. Rather, Shannon made the key observation that the source of information should be modeled as a random process and proposed entropy (average log probability) as the measure of information content.
Shannon’s source coding theorem states that the average number of bits per symbol necessary to uniquely describe any data source can approach the corresponding entropy as closely as desired. This is the best performance one can hope for in lossless compression. For the case where some error is allowed without impacting semantics (lossy compression), Shannon developed the rate-distortion theory, which describes the fundamental trade-off between fidelity and compression ratio.
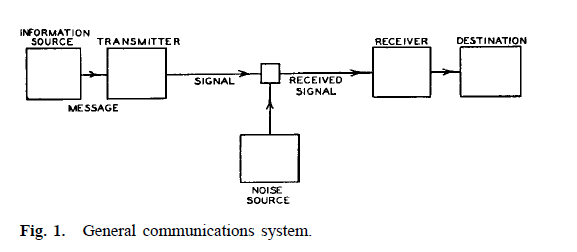
2) Shannon abstracted the communication problem as shown in Appendix 1, where the ‘channel’ accounts for any corruption of the sent messages during communication and the ‘transmitter’ is used to add redundancy to combat the corruption. This idea was revolutionary in a world where modulation was generally thought of as an effectively memoryless process and no error-correcting codes had been invented.
From information theory comes the notion of channel capacity, which is a property of any given communication channel, and proved the channel coding theorem: The error rate of data transmitted over a band-limited noisy channel can be reduced to an arbitrarily small amount if the information rate is lower than the channel capacity. This theorem established the fundamental limit of reliable transmission of information, and was very counterintuitive to the existing community.
The development of information theory ultimately established a solid foundation for those techniques that determine digital communications: data compression, data encryption, and data correction, and gave rise to an enormous and sophisticated communications industry. Today, information theory continues to set the stage for the development of communications, data storage and processing, and other information technologies that are indispensable parts of people’s daily lives.
Features that set this work apart from similar achievements
The development of information theory is more than a breakthrough in a science or engineering field. Due to its revolutionary nature and wide repercussions, it is described as one of humanity’s most remarkable creations, a general scientific theory that profoundly changed the world and how human beings interact with one another.
In particular, information theory transformed communication system engineering, altering all aspects of communication theory and practice.
First of all, Shannon's work introduced the unit ‘bit’ and makes information a measurable quantity just as temperature or energy. He provided a rigorous theory to back up communication engineering, characterized the fundamental limits of communications and transformed it from an art to a science. The theory was general and applicable to the various communication systems that were dealt with using entirely different tools in the pre-Shannon era.
Shannon’s definition of information was intuitively satisfying, but his theory was not without surprises. Before the development of information theory, it was widely believed that to achieve arbitrarily small error probability in transmission, arbitrarily large bandwidth or arbitrarily high power was necessary. Shannon proved this intuitive belief wrong. He was able to show that any given communication channel has a maximum capacity for transmitting information; if the information rate of the source is smaller than that capacity, messages can be sent with vanishingly low error probability when properly encoded.
Moreover, information theory is not just a mathematical theory. In fact, it is hard to overestimate its practical implications. In his famous channel coding theorem, Shannon predicted the role of forward error correction schemes, and this spawned a separate area of investigation in the course of time within digital communications, namely: the coding theory. Nowadays, error correction codes are an indispensable part of essentially all contemporary communication systems.
Significant references
Theses:
[A1] C.E.Shannon, A Symbolic Analysis of Relay and Switching Circuits, Master's Thesis http://dspace.mit.edu/bitstream/handle/1721.1/11173/34541425-MIT.pdf?sequence=2
[A2] C.E.Shannon, An Algebra for Theoretical Genetics, Doctoral Thesis http://dspace.mit.edu/bitstream/handle/1721.1/11174/34541447-MIT.pdf?sequence=2
Scholarly Journal Articles:
[B1] C.E.Shannon, A Mathematical Theory of Communication, The Bell System Technical Journal, volume 27, pp.379-423, 623-656, July, October, 1948 (Republished as a monograph in 1949 by the University of Illinois Press with preface by W. Weaver) http://worrydream.com/refs/Shannon%20-%20A%20Mathematical%20Theory%20of%20Communication.pdf
[B2] C.E.Shannon, Communication Theory of Secrecy Systems, The Bell System Technical Journal, volume 28, pp.656-715, October, 1949 http://netlab.cs.ucla.edu/wiki/files/shannon1949.pdf
[B3] C.E.Shannon, Communication in the Presence of Noise, Proceedings of the IRE, volume 37, No.1, pp. 10-21, January, 1949 http://web.stanford.edu/class/ee104/shannonpaper.pdf
[B4] J.R.Pierce, The Early Days of Information Theory, IEEE Transactions on Information Theory, Vol IT-19, No.1, pp. 3-8, January, 1973 http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=1054955
[B5] F.Ellersick, A Conversation with Claude Shannon, IEEE Communications Magazine, Vol.22 No.5, May, 1984 http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=1091957
[B6] Sergio Verdú, Fifty Years of Shannon Theory, IEEE Transactions on Information Theory, Vol.44, No. 6, pp. 2057-2078, October, 1998 http://www.princeton.edu/~verdu/reprints/IT44.6.2057-2078.pdf
[B7] Wilfried Gappmair, Claude E.Shannon: the 50th Anniversary of Information Theory, IEEE Communications Magazine, April, 1999 http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=755458
[B8] Samuel W. Thomsen, Some Evidence Concerning the Genesis of Shannon's Information Theory, Studies in History and Philosophy of Science 40 (2009) 81-91 http://ac.els-cdn.com/S0039368108001143/1-s2.0-S0039368108001143-main.pdf?_tid=ef7f753e-316f-11e5-9091-00000aacb361&acdnat=1437679433_91e28c707ddff6fa12a9cf89ced468e8
[B9] C. E. Shannon, R. G. Gallager, and E. R. Berlekamp, Lower bounds to error probability for coding on discrete memoryless channels I, Information and Control, 10, 65-103, 1967. http://ac.els-cdn.com/S0019995867900526/1-s2.0-S0019995867900526-main.pdf?_tid=ef3499a0-5191-11e5-9f2c-00000aab0f01&acdnat=1441212473_e597ba5b84b4adb8b037b9c6a44c957a
Books:
[C1] Paul J. Nahin, The Logician and the Engineer, Princeton University Press, 2012
[C2] James Gleick, The Information: A History, A Theory, A Flood, Pantheon Books, New York, 2011
[C3] N. J. A. Sloane and A. D. Wyner, Claude Elwood Shannon Collected Papers, IEEE Press, Piscataway, NJ, 1993
News Articles:
Miscellaneous:
[E1] C.E.Shannon, Letter to Vannevar Bush, February 16, 1939 http://ieeexplore.ieee.org/xpl/ebooks/bookPdfWithBanner.jsp?fileName=5311546.pdf&bkn=5271069&pdfType=chapter
[E2] John R. Pierce, Looking Back - Claude Elwood Shannon, IEEE Potentials, December 1993 http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=282341
[E3] Eugene Chiu, Jocelyn Lin, Brok Mcferron, Noshirwan Petigara, Satwiksai Seshasai, Mathematical Theory of Claude Shannon, 6.933J/STS.420J The Structure of Engineering Revolutions, MIT, 2001 http://web.mit.edu/6.933/www/Fall2001/Shannon1.pdf
[E4] Ioan James FRS, Claude Elwood Shannon: 30 April 1916 - 24 February 2001, Biographical Memoirs of Fellows of the Royal Society http://rsbm.royalsocietypublishing.org/content/roybiogmem/55/257.full.pdf?
[E5] Bernard Dionysius Geoghegan, The Historic Conceptualization of Information: A Critical Survey, IEEE Annals of the History of Computing, 30(1), 66-81 http://pages.uoregon.edu/koopman/courses_readings/phil123-net/intro/Geoghegan_HistoriographicConception_information.pdf
Awards:
Claude Shannon received dozens of major professional awards and other forms of recognition over his career, which are also testimony to the extraordinary importance of his development of information theory, to which he devoted his career. Below are a few examples; a more extensive list can be found in Shannon’s wikipedia entry https://en.wikipedia.org/wiki/Claude_Shannon .
[F1] Stuart Ballatine Medal, 1955
[F2] IEEE Medal of Honor, 1966
[F3] National Medal of Science, 1966
[F4] IEEE Claude E. Shannon Award, 1972
[F5] Harvey Prize, 1972
[F6] Harold Pender Award, 1978
[F7] John Fritz Medal, 1983
[F8] Elected to National Academy of Engineering, 1985
[F9] Kyoto Prize, 1985
[F10] National Inventors Hall of Fame, 2004